INFINITEsimal
The research studio investigated non-linear algorithmic procedures at both a methodological and tectonic level by studying the fourth spatial dimension. This project proposes a hybrid program of an archive and a spiritual function, exploring the idea of infinity and how they can be experienced conceptually and spatially.
The following postulates form the framework of the investigation:
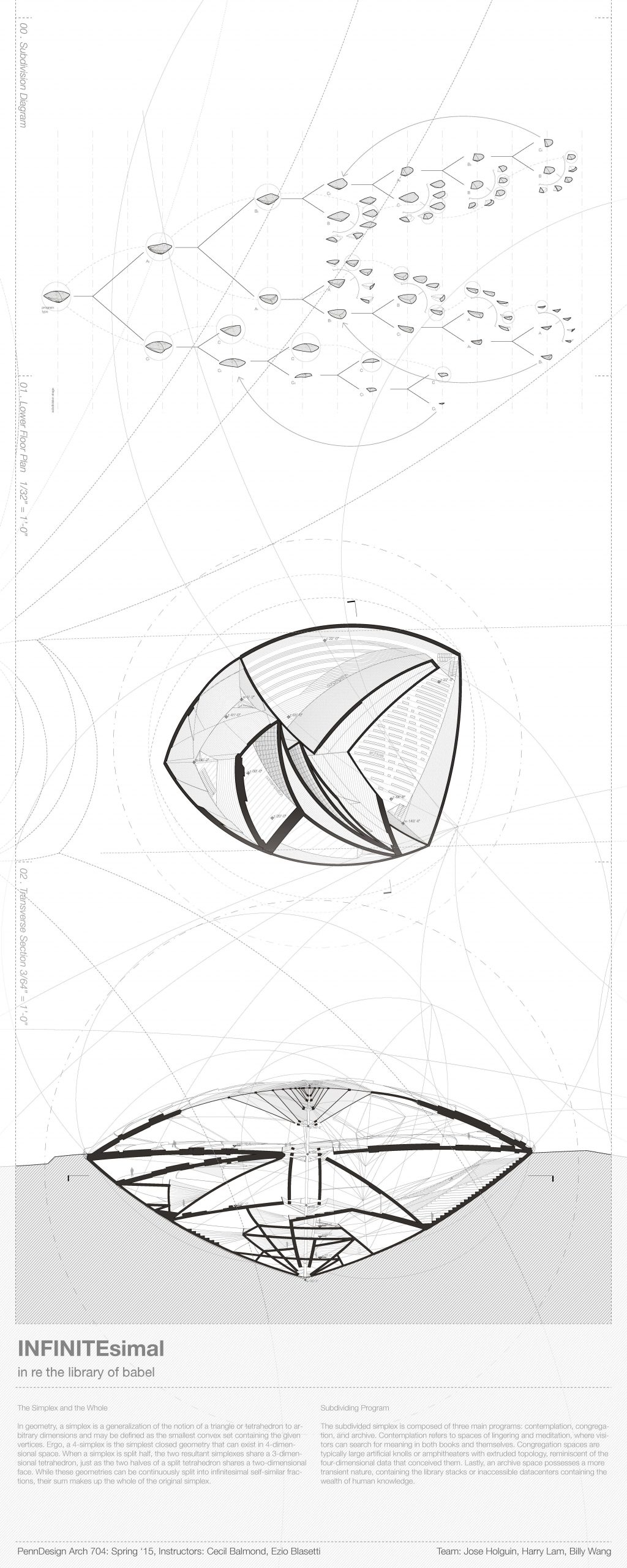
1. The fourth spatial dimension can be described as an extrusion of our three-dimensional world in a direction perpendicular to the perceivable three (the most basic geometry being the simplex, the equivalent of a triangle in 2D). Thus, our reality is merely an infinitesimal slice of the compounded folds in space-time. Similarly, one could allude to the current collection of human knowledge as merely a slice of the infinite continuum of universal understanding.
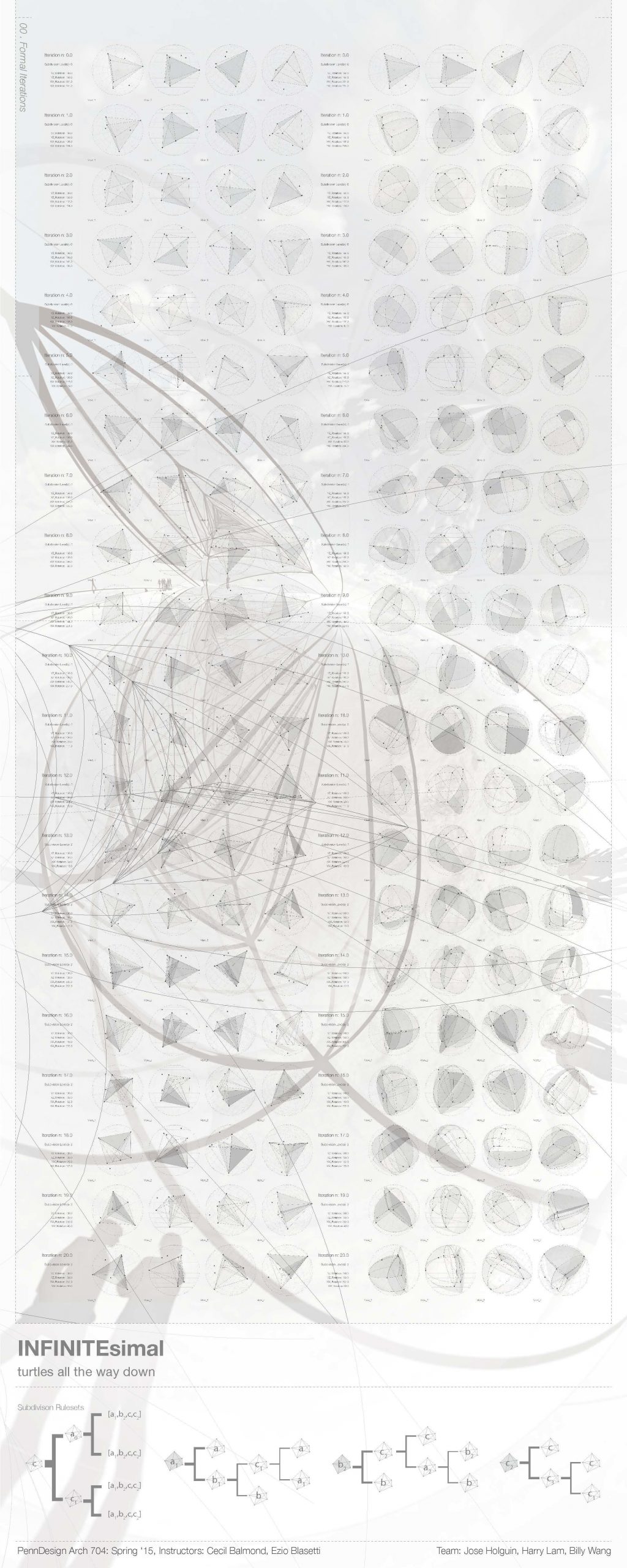
2. Illustrated in Zeno’s paradox, “Achilles and the Tortoise,” recursive subdivision may be used as a method of creating a virtual infinitude within a finite geometry. These self-similar geometries inevitably converge to points of infinitesimal size.
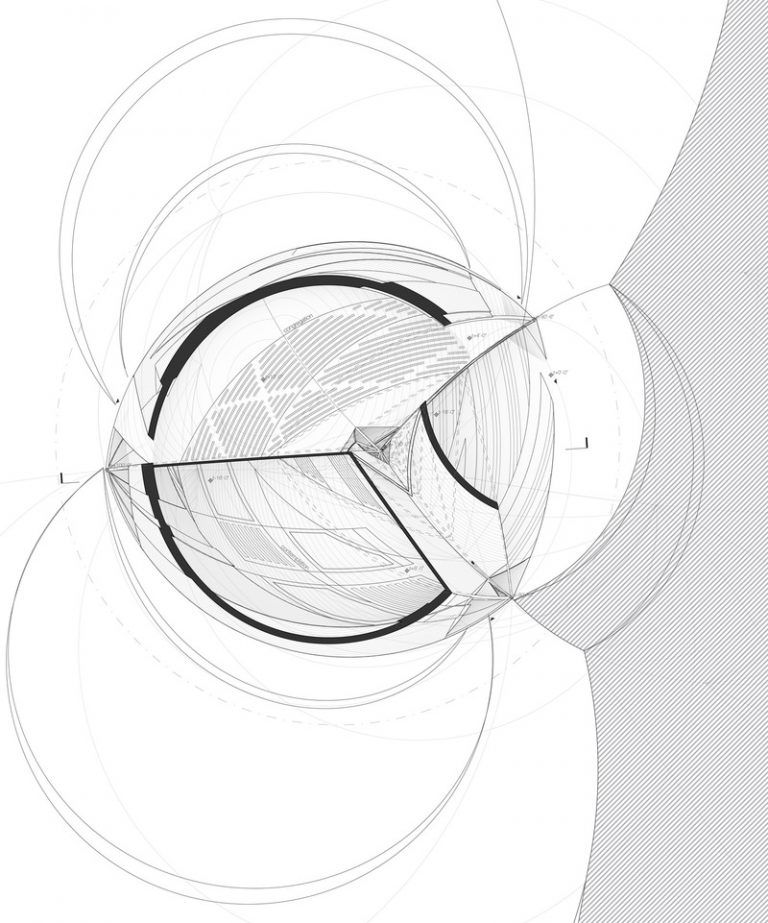
3. In order to perceive a four-dimensional geometry, one may utilize contours or other projection methods. The “point at infinity,” used in stereographic projection creates a vanishing “horizon” as the geometry approaches the point of projection.
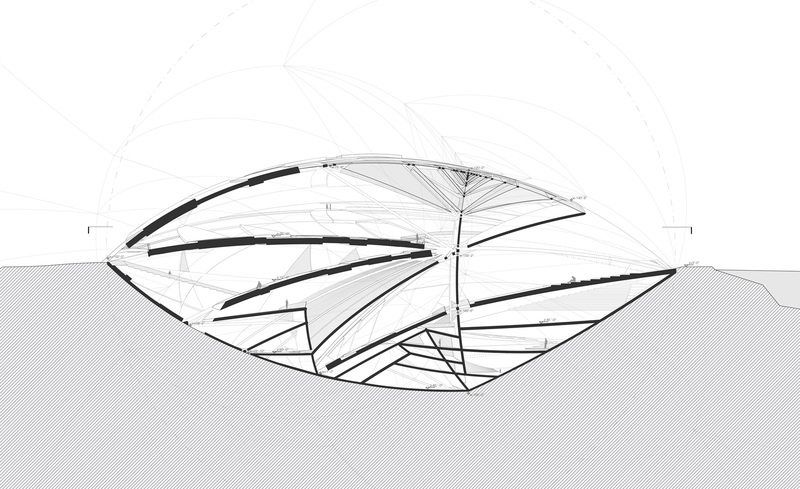
The design describes a simplex subdivided by a ruleset which created points of convergence. Once projected into three-dimensions, the resultant geometry, a distorted tetrahedron, is characterized by dramatic curves and natural vanishing points at each of its vertices. These draw the occupants visually to the designated points of access and subsequently, the adjoining volume(s). As one wanders deeper into the spiraling labyrinth, one feels both a sense of compression as well as infinitude.
“I have just written the word “infinite.” I have not interpolated this adjective out of rhetorical habit; I say that it is not illogical to think that the world is infinite. Those who judge it to be limited postulate that in remote places the corridors and stairways and hexagons can conceivably come to an end — which is absurd. Those who imagine it to be without limit forget that the possible number of books does have such a limit. I venture to suggest this solution to the ancient problem: The Library is unlimited and cyclical.”
– Jorge Luis Borges in “The Library of Babel”
Project Credits:
Project Name: INFINITEsimal
Members : Jose Holguin ,Harry Lam & Billy Wang
School: University of Pennsylvania, PennDesign
Advisers: Cecil Balmond & Ezio Blasetti
Arch2o has received this project from our readers in order to participate in the Students week 8 event, you may submit your own work for publication in the Students Week 9 , for more details please CLICK HERE
